An ideal subroutine is a mathematical function; it takes inputs and returns the results of its computation. It has a single entry point and all data local to it is initialized upon entry and cleaned up when it returns to the caller. The next call, if any, starts all over again and no local residues are carried over from the last invocation. A coroutine, is an interesting deviation from these conventions. It can yield control back to the caller as soon as there are partial results that can be put to use. Moreover, when invoked again, it can resume the computation from where it left. These yield/resume semantics make coroutines a better unit of structuring programs for certain types of problems.

This page is an introduction to writing coroutines in C++ using the Boost.Coroutine library.

Python xrange

Consider writing the Python built-in function xrange which takes a number n returns a sequence of numbers from 0 to n without actually storing them all simulatenously. An ideal subroutine cannot do this and we’d need either a functor that holds state between invocations or a coroutine. Here’s the latter:

#include <boost/bind.hpp>
#include <boost/coroutine/coroutine.hpp>

// The coroutine type.
typedef boost::coroutines::coroutine<int()> coro;

// The implementation routine of the coroutine.
void xrange_impl(coro::caller_type& yield, int limit)
{
  for(int i = 0; i < limit; i++) {
    yield(i); // return results back to the caller
  }
}

int main()
{
  // Construct the coroutine instance
  coro xrange(boost::bind(xrange_impl, _1, 10000));

  int sum = 0;
  while(xrange) { // Check completion status
    sum += xrange.get(); // Extract yielded result
    xrange(); // Fire it again.
  }
  assert(sum == 49995000);
}

Here’s a (not so) quick walkthrough of the code:

We start by defining our coroutine type by instantiating the boost::coroutines::coroutine template class with the logical signature of the generator. This logical signature, here, is int() because our coroutine is expected to generate integers. The complete type (which we typedef as coro to save some typing) is thus, boost::coroutines::coroutine<int()>.

Next, we provide the real implementation of the coroutine as the xrange_impl function. This function is meant to be invoked repeatedly and is expected to yield the next number in the sequence back to its caller. Remember, that coroutines operate in pairs, so a coroutine (unlike a subroutine) does not return a value back to its caller, instead, it calls the caller back with the result. The first parameter that the implementation routine takes is a reference to that calling coroutine. I usually name that parameter yield to signify its usage.

The complete type of this calling coroutine is the inverse of the type of the coroutine we’re writing. For the xrange example, where we’re writing a coroutine that generates integer values, the inverse coroutine is one that consumes integer values, i.e. boost::coroutines::coroutine<void(int)>. We don’t need to compute this inverse type ourselves because the coroutine type conveniently provides it as a member typedef caller_type. The implementation function is allowed to take other parameters (like limit in our case) but those must be bound to their values at the time of the coroutine construction (like we do in main.)

Next, with the coroutine instance ready, we iterate over it to extract the values it yields. This is done using the xrange.get() function (its return type is the return type of the logical signature of the coroutine, i.e. int). Coroutine completion can be checked using the implicit boolean conversion operator and the next invocation can be triggered by invoking the function call operator (it takes the same parameters as the logical signature.)

With these in place, our C++ xrange routine is done. Let’s take on a slightly more complicated generator.

Same Fringe

Consider the problem of writing a routine that checks if two binary trees have the same fringe i.e. if they have exactly the same leaves reading from left to right. To illustrate, all the blue trees below have the same fringe while none of them have the same fringe as the red one.

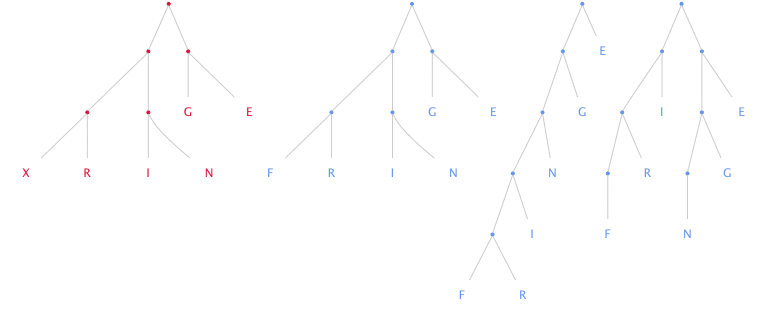
How would we write a routine that takes two binary trees and checks if they have the same fringe?

Simple, check if the post-order traversals of the two trees are the same. That works, but is suboptimal as it requires us to access all leaf nodes in both the trees, always. Looking at all nodes is necessary before returning a true but we should be able to return false sooner. For example, given the red and any of the blue trees from above, we can return a false after looking at just the first node from the two trees. To do that we would have to compare the trees one leaf at a time. The routine would have to descend down to the first leaf and yield control back to the caller with the leaf value. The caller would then compare the values of two leaves received and return false if they don’t match or return control back to the routines to resume their traversals. Pause a little while here and consider writing a subroutine that can do this.

The example, though academic, gives us insight that a coroutine based generator is better when it makes sense to return partial results early and resume the remaining computation only if needed. Here’s how we do that for the problem above:

#include <misc/tree.hpp>
#include <boost/bind.hpp>
#include <boost/coroutine/all.hpp>

typedef ajd::binary_tree<char> tree;
typedef boost::coroutines::coroutine<char()> generator;

bool is_leaf(tree::node l) { return !(l->left || l->right); }

void next_leaf(generator::caller_type& yield, tree::node& node)
{
  if(node) {
    next_leaf(yield, node->left);
    next_leaf(yield, node->right);
    if(is_leaf(node)) { yield(node->value); }
  }
}

bool same_fringe(tree::node one, tree::node two)
{
  generator leaf1(boost::bind(next_leaf, _1, one));
  generator leaf2(boost::bind(next_leaf, _1, two));
  for(; leaf1 && leaf2; leaf1(), leaf2()) {// iterate till *both* traversal are active
    if(leaf1.get() != leaf2().get()) {// compare the next leaf node
      return false;// return false, if they don't match.
    }
  }
  if(leaf1 || leaf2) {// if one of the traversals is still active,
    return false;// one tree has more leaves than the other.
  }
  return true;
}

int main()
{
  tree::node empty = tree::read_tree("");
  tree::node red = tree::read_tree("(-(-(-(X)(R))(-(I)(N)))(-(G)(E)))");
  tree::node blue1 = tree::read_tree("(-(-(-(F)(R))(-(I)(N)))(-(G)(E)))");
  tree::node blue2 = tree::read_tree("(-(-(-(-(-(F)(R))(I))(N))(G))(E))");
  tree::node blue3 = tree::read_tree("(-(-(-(-()(F))(R))(I))(-(-(-(N)())(G))(E))");
  tree::node diff = tree::read_tree("(-(-(-(-()(F))(R))(I))(-(-(-(N)())(G))())");
  assert(!same_fringe(empty, red));
  assert(!same_fringe(red, blue1));
  assert(same_fringe(empty, empty));
  assert(same_fringe(blue1, blue2));
  assert(same_fringe(blue2, blue3));
  assert(!same_fringe(blue2, diff));
}

The logical type of the coroutine here is char() because it is expected to generate char values contained in the leaf nodes. The function next_leaf is the implementation function that traverses a tree recursively and yields the leaf node values in post-order. The tree instance it has to traverse is passed along with the required caller_type& parameter. The same_fringe routine instantiates the two generators and binds them to the two trees under consideration. Then it extracts the leaves and compares them to ensure that we return false as soon as we’re certain that the fringes differ. In the best case, we return after just one node comparison and that is something that is difficult to achieve without using coroutines.

So then, dear reader, that just about does it for my introduction to coroutines. Hope you found it useful.